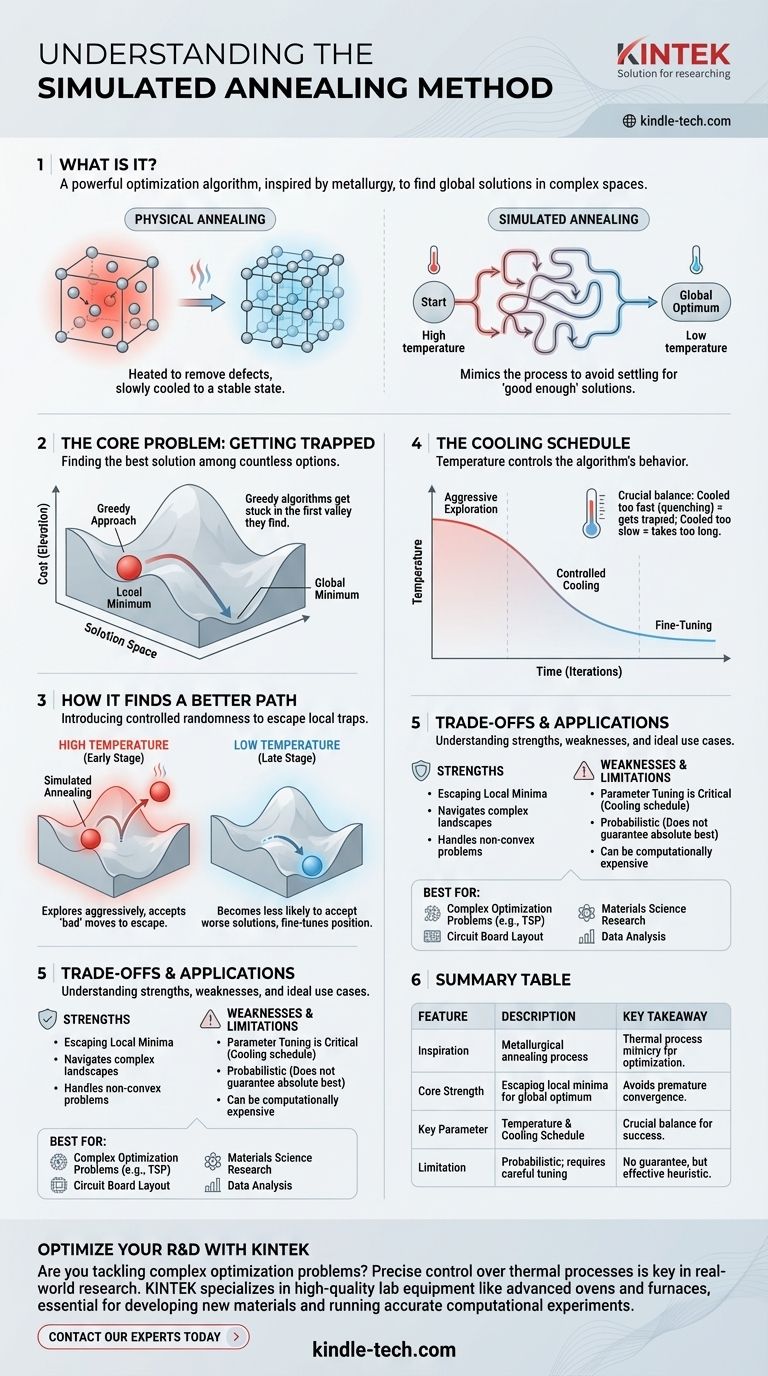
En resumen, el recocido simulado es un potente algoritmo de optimización utilizado para encontrar una solución buena (y a menudo global) en un espacio de búsqueda vasto y complejo. Se inspira directamente en el proceso metalúrgico de recocido, donde un material se calienta y luego se enfría lentamente para eliminar defectos y alcanzar un estado cristalino estable y de baja energía. El algoritmo imita este proceso físico para resolver problemas computacionales abstractos.
En esencia, el recocido simulado evita la trampa común de conformarse con una solución "suficientemente buena" imitando el proceso físico de recocido del metal. Comienza explorando una amplia gama de posibilidades (alta temperatura) y gradualmente reduce su enfoque a una solución estable y de alta calidad (baja temperatura).
El problema central: Quedarse atrapado
Para entender el recocido simulado, primero debe entender el problema que resuelve: encontrar la mejor solución posible entre innumerables opciones, una tarea conocida como optimización.
El panorama de soluciones
Imagine que cada solución posible a su problema es un punto en un vasto paisaje montañoso. La elevación de cada punto representa su "costo": cuanto menor sea la elevación, mejor será la solución. Su objetivo es encontrar el punto más bajo de todo el mapa, el mínimo global.
El enfoque "codicioso" y su defecto
Un algoritmo simple, a menudo llamado ascenso de colinas (hill-climbing), comenzaría en un punto aleatorio y siempre se movería cuesta abajo. Este es un enfoque "codicioso" porque solo acepta movimientos que producen una mejora inmediata.
El problema es que este método se quedará atascado en el primer valle que encuentre, un mínimo local. No tiene forma de saber si un valle mucho más profundo, el mínimo global, existe justo al otro lado de la siguiente colina.
Cómo el recocido simulado encuentra un camino mejor
El recocido simulado supera esta limitación introduciendo un elemento controlado de aleatoriedad que le permite escapar de estas trampas locales.
La inspiración: Recocido físico
En metalurgia, calentar un metal da a sus átomos suficiente energía para moverse libremente, saliendo de estructuras subóptimas y defectuosas. A medida que el metal se enfría lentamente, los átomos tienen tiempo de asentarse en una red cristalina altamente ordenada y fuerte, un estado de energía mínima.
El algoritmo: La temperatura como mando de control
El recocido simulado adopta este concepto introduciendo un parámetro de temperatura. Esta no es una temperatura física, sino una variable que controla el comportamiento del algoritmo.
El algoritmo comienza con una temperatura alta. En este estado, explora el panorama de soluciones de forma agresiva, muy parecido a los átomos energéticos en el metal caliente. Tiene una alta probabilidad de aceptar movimientos que son peores que su posición actual. Esta es la clave: hacer un movimiento "malo" es lo que le permite salir de un mínimo local.
El programa de enfriamiento
A medida que el algoritmo se ejecuta, la temperatura se reduce gradualmente según un programa de enfriamiento. A medida que la temperatura disminuye, el algoritmo se vuelve cada vez menos propenso a aceptar una solución peor.
Al final, a una temperatura muy baja, el algoritmo se comporta como el método simple de ascenso de colinas, solo aceptando mejoras y ajustando su posición en lo que se espera sea el mínimo global.
Comprendiendo las compensaciones
Como cualquier herramienta potente, el recocido simulado no es una solución universal. Comprender sus limitaciones es fundamental para usarlo de manera efectiva.
Fortaleza: Escapar de mínimos locales
Su principal ventaja es su capacidad para navegar por paisajes complejos y no convexos con muchos mínimos locales. Para problemas en los que los algoritmos codiciosos fallan sistemáticamente, el recocido simulado es una excelente opción.
Debilidad: La sintonización de parámetros es crítica
El rendimiento del algoritmo es muy sensible al programa de enfriamiento. Si se enfría demasiado rápido, puede quedar atrapado en un mínimo local de todos modos ("temple"). Si se enfría demasiado lento, puede llevar una cantidad de tiempo poco práctica encontrar una solución. Encontrar el programa adecuado a menudo requiere experimentación.
Limitación: Es un método probabilístico
El recocido simulado no garantiza que encontrará la mejor solución absoluta (el mínimo global). Es una heurística, lo que significa que está diseñado para encontrar una muy buena solución en un tiempo razonable. Siempre existe una posibilidad estadística de que se asiente en un estado subóptimo.
Tomar la decisión correcta para su problema
Utilice esta guía para decidir si el recocido simulado es el enfoque correcto para su tarea de optimización.
- Si su objetivo principal es resolver un problema complejo con muchas trampas (mínimos locales): El recocido simulado es una de las mejores herramientas para el trabajo, especialmente para problemas clásicos como el Problema del Viajante o el diseño de placas de circuitos.
- Si su objetivo principal es encontrar una solución demostrablemente óptima con la máxima velocidad: Primero debe verificar si su problema es lo suficientemente simple (por ejemplo, convexo) como para ser resuelto por un algoritmo determinista más rápido, como la programación lineal o un enfoque codicioso estándar.
En última instancia, el recocido simulado proporciona un marco robusto para navegar por espacios de búsqueda vastos y difíciles para encontrar soluciones de alta calidad donde los métodos más simples fallan.
Tabla resumen:
| Característica | Descripción |
|---|---|
| Inspiración | Proceso de recocido metalúrgico (calentamiento y enfriamiento lento) |
| Principal fortaleza | Escapar de mínimos locales para encontrar un óptimo global |
| Parámetro clave | Temperatura y programa de enfriamiento |
| Mejor para | Problemas de optimización complejos con muchas trampas locales |
| Limitación | Probabilístico; requiere una cuidadosa sintonización de parámetros |
Optimice su investigación y desarrollo con KINTEK
¿Está abordando problemas complejos de optimización en ciencia de materiales, ingeniería química o análisis de datos? Los principios del recocido simulado se inspiran en procesos térmicos del mundo real, y tener un control preciso sobre esos procesos en su laboratorio es crucial.
KINTEK se especializa en equipos de laboratorio de alta calidad, incluidos hornos y estufas avanzados que proporcionan el calentamiento uniforme y el enfriamiento controlado esenciales para la investigación y el desarrollo. Ya sea que esté desarrollando nuevos materiales o realizando experimentos computacionales, un equipo confiable es la base de resultados precisos.
Contacte a nuestros expertos hoy para encontrar la solución de laboratorio perfecta para mejorar sus flujos de trabajo de optimización y lograr resultados innovadores.
Productos relacionados
- Horno de atmósfera de hidrógeno
- Pequeño horno de sinterización de alambre de tungsteno al vacío
- Horno de atmósfera controlada con cinta de malla
- 1400℃ Horno de atmósfera controlada
- Equipo HFCVD con revestimiento de nanodiamante y troquel de trefilado
La gente también pregunta
- ¿Cuál es un ejemplo de atmósfera reductora?Aplicaciones en acero y cerámica
- ¿Qué es la atmósfera del horno?Claves para el éxito del procesamiento de materiales
- ¿Cuál es el uso del hidrógeno en el horno? Una clave para el procesamiento a alta temperatura sin oxígeno
- ¿Cuándo necesitaría usar una atmósfera controlada? Para prevenir la contaminación y controlar las reacciones
- ¿Qué precauciones de seguridad debe tomar al trabajar con una fuente de calor? Directrices esenciales para un entorno de laboratorio seguro
