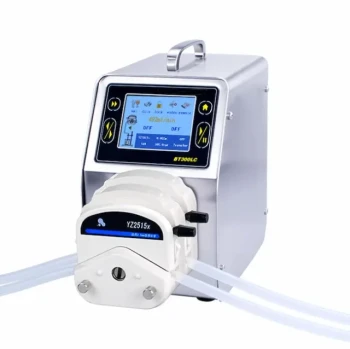
En esencia, la relación entre las fuerzas en un sistema hidráulico se rige por la Ley de Pascal, que permite que una pequeña fuerza de entrada se multiplique en una fuerza de salida significativamente mayor. Este principio de multiplicación de fuerza se logra aplicando presión a un fluido confinado e incompresible, como el aceite.
La relación fundamental es que la presión permanece constante en todo un sistema hidráulico cerrado. Al manipular el área de la superficie sobre la que actúa esta presión, se puede intercambiar directamente una pequeña fuerza aplicada sobre un área pequeña por una gran fuerza generada sobre un área grande.
El principio central: la ley de Pascal
Toda la base de la potencia hidráulica se basa en un principio simple descubierto en el siglo XVII. Comprender esto es clave para entender cómo funciona toda la maquinaria hidráulica, desde los frenos de un automóvil hasta una prensa de 300 toneladas.
¿Qué es la Ley de Pascal?
La Ley de Pascal establece que un cambio de presión en cualquier punto de un fluido confinado e incompresible se transmite por igual en todo el fluido. En términos más sencillos, si empujas el fluido en un punto, la presión en todas partes dentro del recipiente aumenta en la misma cantidad.
El papel de la presión
La presión se define como Fuerza dividida por Área (P = F/A). Esta simple fórmula es la clave para desbloquear la multiplicación de la fuerza. Al controlar el área, puede influir directamente en la fuerza.
Cómo se multiplica la fuerza
Imagine un recipiente sellado con dos pistones de diferentes tamaños: un pistón de entrada pequeño (Área 1) y un pistón de salida grande (Área 2).
Cuando aplica una fuerza pequeña (Fuerza 1) al pistón pequeño, genera presión (Presión = Fuerza 1 / Área 1).
Debido a que esta presión se transmite por igual a través del fluido, la misma presión empuja hacia arriba sobre el pistón de salida grande. Esto crea una fuerza de salida mucho mayor (Fuerza 2 = Presión x Área 2).
Dado que la presión es la misma, podemos decir F1/A1 = F2/A2. Esta ecuación muestra que la fuerza de salida (F2) es directamente proporcional a la relación de las áreas. Si el pistón de salida tiene 10 veces el área del pistón de entrada, obtendrá 10 veces la fuerza.
Comprender las compensaciones
La multiplicación de la fuerza no crea energía de la nada. Esta poderosa ventaja conlleva compromisos inherentes que son críticos de entender en cualquier aplicación práctica.
La compensación entre fuerza y distancia
La compensación más significativa es entre la fuerza y la distancia que debe recorrer el pistón. Para mover el pistón de salida grande una distancia pequeña, el pistón de entrada pequeño debe empujarse una distancia mucho mayor.
El trabajo (energía) se calcula como Fuerza por Distancia. El trabajo realizado en el lado de entrada debe ser igual al trabajo realizado en el lado de salida (ignorando la fricción). Si multiplica la fuerza por 10, también debe multiplicar la distancia de recorrido del pistón de entrada por 10 para lograr el mismo recorrido de salida.
Eficiencia y pérdidas del mundo real
La fórmula F1/A1 = F2/A2 describe un sistema perfecto y sin fricciones. En realidad, siempre tendrá pérdidas de eficiencia.
La fricción entre los sellos y las paredes del cilindro, así como la fricción interna (viscosidad) del fluido hidráulico, reducirán ligeramente la fuerza de salida real. Un sistema bien diseñado suele tener más del 90% de eficiencia, pero nunca es un perfecto 100%.
El elemento de control
La potencia bruta es inútil sin la capacidad de gestionarla. Simplemente aplicar fuerza a un pistón no le da precisión sobre la velocidad o la magnitud de esa fuerza.
Aquí es donde componentes como las válvulas de control proporcional y los controles de bomba proporcionales se vuelven esenciales. No generan la fuerza, pero regulan con precisión el caudal y la presión del fluido, lo que permite a un operador controlar finamente la velocidad y la fuerza del actuador hidráulico para tareas complejas.
Tomar la decisión correcta para su objetivo
Comprender esta relación de fuerza le permite evaluar el diseño del sistema en función de su objetivo principal.
- Si su enfoque principal es maximizar la salida de fuerza: El objetivo es diseñar un sistema con la mayor relación posible entre el área de salida y el área de entrada.
- Si su enfoque principal es la velocidad: Es posible que deba aceptar un factor de multiplicación de fuerza menor (una relación de área más pequeña) o utilizar una bomba de gran volumen para mover la cantidad requerida de fluido más rápido.
- Si su enfoque principal es la precisión y el control: La ventaja mecánica es solo la mitad de la ecuación; la efectividad de su sistema dependerá de válvulas y controles de alta calidad para modular con precisión la presión y el flujo hidráulicos.
Comprender este equilibrio entre presión, área y desplazamiento es el primer paso para dominar la aplicación de la potencia hidráulica.
Tabla de resumen:
| Concepto | Fórmula clave | Implicación práctica |
|---|---|---|
| Ley de Pascal | La presión se transmite por igual | La pequeña fuerza de entrada crea una gran fuerza de salida |
| Multiplicación de fuerza | F1/A1 = F2/A2 | La fuerza de salida escala con la relación de área |
| Compensación | Trabajo de entrada = Trabajo de salida | El aumento de la fuerza requiere un aumento de la distancia de entrada |
| Eficiencia | Típicamente >90% | Los sistemas del mundo real tienen en cuenta las pérdidas por fricción |
¿Listo para aprovechar la potencia hidráulica precisa para su laboratorio? En KINTEK, nos especializamos en equipos y consumibles de laboratorio de alto rendimiento, asegurando que sus sistemas hidráulicos funcionen con la máxima eficiencia y control. Ya sea que necesite componentes confiables o asesoramiento experto sobre la multiplicación de fuerza para sus aplicaciones, nuestro equipo está aquí para ayudarlo. Contáctenos hoy para optimizar sus soluciones hidráulicas.
Guía Visual
Productos relacionados
- Bomba Peristáltica de Velocidad Variable
- Molde de Prensado Cilíndrico con Escala para Laboratorio
- Reactores personalizables de alta presión para aplicaciones científicas e industriales avanzadas
- Molde de Prensado de Polígonos para Laboratorio
- Molde de Prensa Cuadrado para Aplicaciones de Laboratorio
La gente también pregunta
- ¿Para qué puedo usar una bomba de vacío? Impulsando procesos industriales desde el envasado hasta la automatización
- ¿Cuál es la función principal de una bomba de vacío? Eliminar moléculas de gas para crear un vacío controlado
- ¿Cuáles son las ventajas de usar bombas de vacío de diafragma sin aceite? Logre un vacío limpio y de bajo mantenimiento
- ¿Cuáles son los usos comunes de las bombas de vacío en los laboratorios? Esenciales para Filtración, Evaporación y Análisis
- ¿Cómo se inspecciona una bomba de vacío? Una guía paso a paso para asegurar el máximo rendimiento
