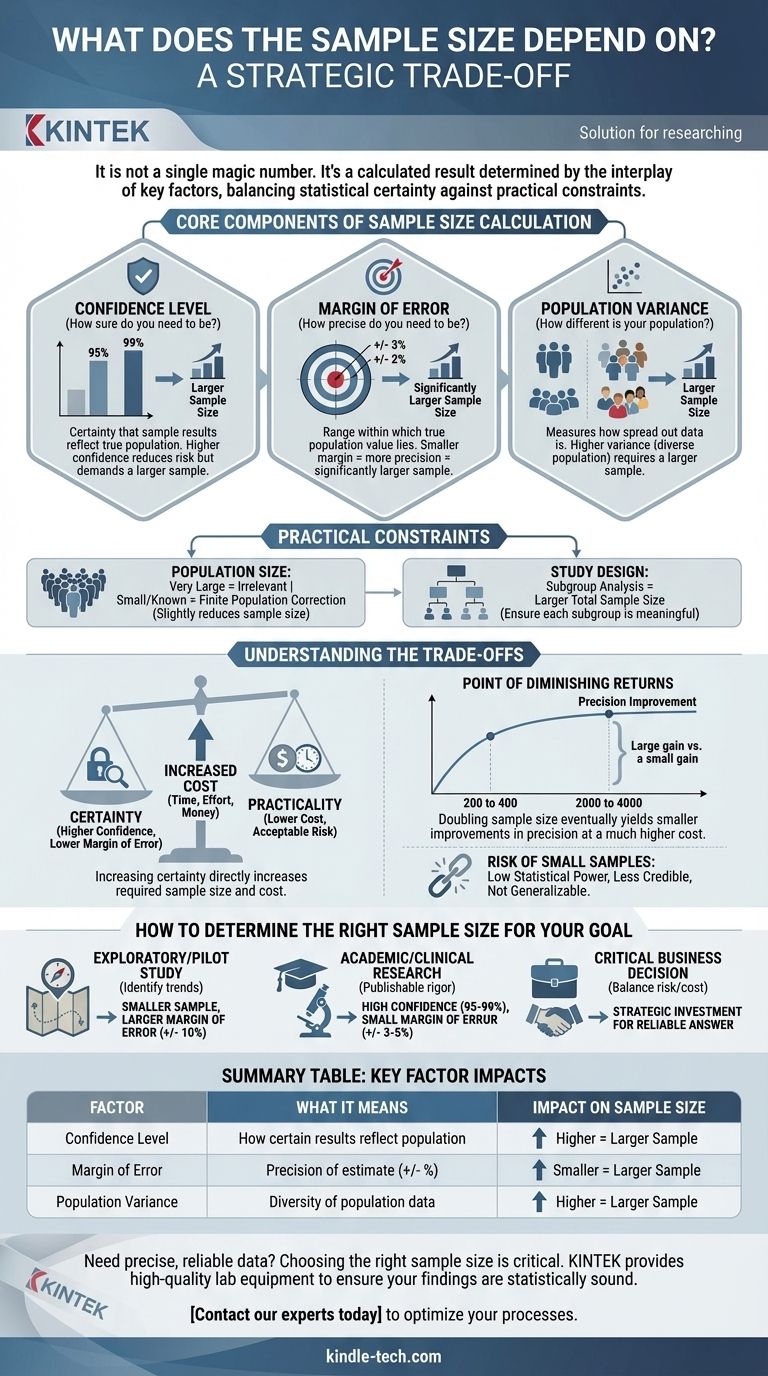
Para ser claros, el tamaño de muestra requerido no es un número mágico único. Es un resultado calculado determinado por la interacción entre el nivel de precisión deseado, su tolerancia al riesgo y la variabilidad inherente de la población que está estudiando. Los tres factores principales que debe definir son su margen de error, su nivel de confianza y la varianza poblacional esperada.
La conclusión principal es que elegir un tamaño de muestra es una decisión estratégica. Está equilibrando la necesidad de certeza estadística (precisión y confianza) con las limitaciones prácticas de sus recursos, como el tiempo y el presupuesto.
Los componentes centrales del cálculo del tamaño de la muestra
Para determinar el tamaño de muestra apropiado, primero debe definir los parámetros de su investigación. Cada uno de los siguientes componentes influye directamente en el cálculo final.
Nivel de confianza (¿Qué tan seguro necesita estar?)
El nivel de confianza le indica qué tan seguro puede estar de que los resultados de su muestra reflejan a la población real. Por lo general, se expresa como un porcentaje, como el 95% o el 99%.
Un nivel de confianza del 95% significa que si repitiera el estudio 100 veces, esperaría que los resultados cayeran dentro de su rango calculado 95 de esas veces.
Los niveles de confianza más altos reducen el riesgo de equivocarse, pero exigen un tamaño de muestra mayor. Este es el precio que paga por una mayor certeza en sus hallazgos.
Margen de error (¿Qué tan preciso necesita ser?)
El margen de error define el rango dentro del cual espera que se encuentre el valor real de la población. Es el valor "+/-" que a menudo ve en los resultados de las encuestas (por ejemplo, "el 45% de los votantes, con un margen de error de +/- 3%").
Un margen de error más pequeño, como +/- 2%, indica una estimación más precisa. Sin embargo, lograr este mayor nivel de precisión requiere un tamaño de muestra significativamente mayor.
Decidir su margen de error implica pensar en las consecuencias de estar equivocado. Para decisiones críticas, un margen de error menor es esencial.
Varianza poblacional (¿Qué tan diferente es su población?)
La varianza poblacional (o desviación estándar) mide cuán dispersos están los datos. En términos sencillos, refleja cuán similares o diferentes son los individuos de su población entre sí.
Si su población es muy uniforme (baja varianza), una muestra más pequeña puede representarla con precisión. Si su población es muy diversa con opiniones o características muy variadas (alta varianza), necesita una muestra más grande para capturar esa diversidad.
Dado que rara vez se conoce la varianza real de antemano, los estadísticos a menudo utilizan una estimación conservadora (p=0.5) para asegurar que la muestra sea lo suficientemente grande.
La influencia de las limitaciones prácticas
Más allá de los principios estadísticos fundamentales, los factores del mundo real también dan forma al tamaño final de su muestra.
Tamaño de la población (¿Siempre importa?)
Para poblaciones muy grandes (por ejemplo, toda la población de un país), el tamaño total deja de ser relevante. La fórmula del tamaño de la muestra se estabiliza y el número que necesita no cambia si la población es de 1 millón o de 100 millones.
Sin embargo, si está estudiando una población pequeña y conocida (por ejemplo, todos los empleados de una empresa específica), puede aplicar una Corrección para Poblaciones Finitas. Esto puede reducir ligeramente el tamaño de muestra requerido.
Diseño y complejidad del estudio
La forma en que diseña su estudio es importante. Si planea analizar subgrupos dentro de su muestra (por ejemplo, comparar respuestas de diferentes grupos de edad), debe asegurarse de que el tamaño de la muestra para cada subgrupo sea lo suficientemente grande como para ser significativo.
Esto a menudo significa que el tamaño total de muestra requerido debe ser mayor que si solo estuviera observando a la población en su conjunto.
Comprender las compensaciones
Elegir un tamaño de muestra es un ejercicio de gestión de prioridades contrapuestas. Comprender las compensaciones inherentes es fundamental para tomar una decisión informada.
El costo de la certeza
Existe una relación directa entre la certeza y el costo. Aumentar su nivel de confianza y disminuir su margen de error siempre aumentará el tamaño de muestra requerido, lo que a su vez aumenta el tiempo, el esfuerzo y el dinero necesarios para su estudio.
El riesgo de las muestras pequeñas
Usar una muestra demasiado pequeña es una gran trampa. Conduce a un bajo poder estadístico, lo que significa que podría no detectar un efecto o diferencia real que realmente existe.
Además, los resultados de muestras insuficientemente dimensionadas son menos creíbles y pueden no ser generalizables a su población, lo que socava todo el propósito de la investigación.
El punto de rendimientos decrecientes
Es crucial reconocer que existe un punto de rendimientos decrecientes. Duplicar su tamaño de muestra de 200 a 400 podría reducir significativamente su margen de error. Sin embargo, duplicarlo de nuevo de 2,000 a 4,000 producirá una mejora mucho menor en la precisión, a un costo mucho mayor.
Cómo determinar el tamaño de muestra correcto para su objetivo
Su elección debe guiarse por el objetivo específico de su investigación.
- Si su enfoque principal es la investigación exploratoria o un estudio piloto: A menudo es aceptable una muestra más pequeña con un margen de error mayor (por ejemplo, +/- 10%) para identificar tendencias generales e informar futuras investigaciones.
- Si su enfoque principal es la investigación académica o clínica: Debe priorizar el rigor con un alto nivel de confianza (95% o 99%) y un margen de error pequeño (por ejemplo, +/- 3-5%) para asegurar que sus hallazgos sean sólidos y publicables.
- Si su enfoque principal es una decisión empresarial crítica: Debe equilibrar el costo de la investigación con el riesgo financiero de tomar una decisión equivocada basada en datos imprecisos.
En última instancia, elegir el tamaño de muestra correcto se trata de invertir estratégicamente sus recursos para obtener la respuesta más fiable a su pregunta más importante.
Tabla de resumen:
| Factor | Lo que significa | Impacto en el tamaño de la muestra |
|---|---|---|
| Nivel de confianza | Qué tan seguro está de que los resultados reflejan a la población | Mayor confianza = Muestra mayor |
| Margen de error | La precisión de su estimación (p. ej., +/- 3%) | Margen menor = Muestra mayor |
| Varianza poblacional | Qué tan diversa o similar es su población | Mayor varianza = Muestra mayor |
¿Necesita datos precisos y fiables para su investigación o control de calidad?
Elegir el tamaño de muestra correcto es fundamental para obtener resultados válidos, ya sea que esté realizando estudios académicos, investigación de mercado o pruebas de materiales. En KINTEK, entendemos que el éxito de su laboratorio depende de datos precisos. Nos especializamos en proporcionar el equipo de laboratorio y los consumibles de alta calidad que necesita para ejecutar su investigación sin errores.
Permítanos ayudarle a optimizar sus procesos. Contacte a nuestros expertos hoy mismo para discutir cómo nuestras soluciones pueden respaldar sus necesidades específicas de laboratorio y garantizar que sus hallazgos sean estadísticamente sólidos.
Productos relacionados
- Molino vibratorio
- Tamiz vibratorio tridimensional húmedo
- Criba vibratoria
- Micro trituradora de tejidos
- Molino vibratorio de disco/taza
La gente también pregunta
- ¿Cuál es el uso del agitador de tamices en el laboratorio? Automatizar el análisis del tamaño de partícula para obtener resultados precisos
- ¿Qué es la máquina de agitación para el análisis granulométrico? Asegure resultados precisos y repetibles del tamaño de partícula
- ¿Cuál es la función de la máquina tamizadora? Logre un análisis preciso del tamaño de las partículas
- ¿Cómo funciona una máquina tamizadora? Logre un análisis preciso del tamaño de partícula
- ¿Cuál es el principio del tamizador vibratorio? Lograr un análisis preciso del tamaño de partícula
