El principio central detrás de una prensa hidráulica es la Ley de Pascal, que permite una inmensa multiplicación de la fuerza utilizando un fluido incompresible. Esta ley establece que cualquier presión aplicada a un fluido dentro de un sistema cerrado se transmite por igual a través de todo el fluido. Una prensa hidráulica explota esto utilizando una pequeña fuerza inicial sobre un área pequeña para generar una fuerza de salida mucho mayor sobre un área más grande.
La idea fundamental es que una prensa hidráulica no crea energía, sino que multiplica la fuerza. Lo logra convirtiendo una pequeña fuerza aplicada sobre un pistón pequeño en una presión en todo el sistema, que luego actúa sobre un pistón más grande para producir una fuerza de salida proporcionalmente mayor.
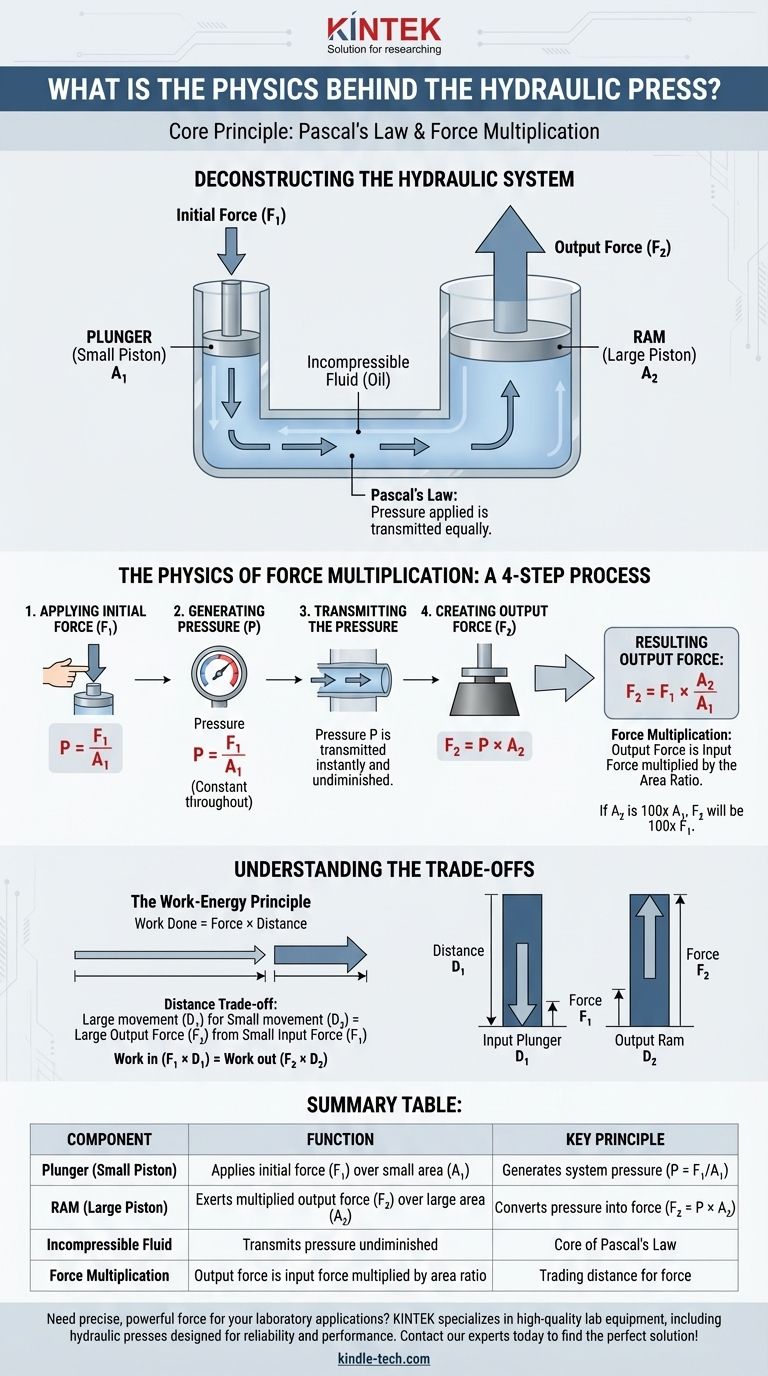
Deconstruyendo el Sistema Hidráulico
Para comprender la física, primero debemos observar los componentes esenciales que componen cualquier prensa hidráulica. Estas partes trabajan juntas en un sistema cerrado para transferir y multiplicar la fuerza.
Los Dos Pistones: Émbolo y Cilindro de Empuje (Ram)
Casi todas las prensas hidráulicas tienen dos pistones de diferentes tamaños. El pistón más pequeño, a menudo llamado émbolo (plunger), es donde se aplica la fuerza inicial más pequeña. El pistón más grande, conocido como cilindro de empuje (ram), es el que ejerce la enorme fuerza de compresión para realizar el trabajo.
El Fluido Incompresible
Los pistones están alojados en cilindros conectados por un canal lleno de un fluido incompresible, generalmente un aceite especializado. "Incompresible" es la propiedad clave: significa que el volumen del fluido no cambia bajo presión. Esto asegura que cuando empuja el fluido en un extremo, este transmite inmediatamente esa fuerza al otro extremo sin ser "aplastado".
La Física de la Multiplicación de la Fuerza
El verdadero ingenio de la prensa hidráulica radica en cómo utiliza la relación entre fuerza, presión y área. El proceso es una aplicación clara y de cuatro pasos de la Ley de Pascal.
Paso 1: Aplicación de la Fuerza Inicial (F₁)
El proceso comienza cuando se aplica una fuerza relativamente pequeña (F₁) al pistón de entrada pequeño, el émbolo. Este pistón tiene un área de superficie pequeña (A₁).
Paso 2: Generación de Presión (P)
Esta fuerza inicial genera presión dentro del fluido hidráulico. La cantidad de presión se define por la fórmula Presión = Fuerza / Área. Por lo tanto, la presión (P) en el sistema se calcula como P = F₁ / A₁.
Paso 3: Transmisión de la Presión
Aquí es donde la Ley de Pascal es fundamental. La ley garantiza que la presión (P) que acaba de crear se transmite instantánea e íntegramente a cada parte del fluido encerrado. La presión que actúa sobre el cilindro de empuje grande es exactamente la misma que la presión bajo el émbolo pequeño.
Paso 4: Creación de la Fuerza de Salida (F₂)
Esta presión constante (P) ahora empuja contra el pistón de salida grande, el cilindro de empuje, que tiene un área de superficie mucho mayor (A₂). La fuerza de salida resultante (F₂) se calcula reorganizando la fórmula de presión: Fuerza = Presión × Área.
Por lo tanto, la fuerza de salida es F₂ = P × A₂.
Dado que sabemos que P = F₁ / A₁, podemos sustituirlo en la segunda ecuación para ver la relación directa: F₂ = (F₁ / A₁) × A₂. Esto se puede simplificar para mostrar que la fuerza de salida es la fuerza de entrada multiplicada por la relación de las áreas: F₂ = F₁ × (A₂ / A₁).
Si el área del cilindro de empuje (A₂) es 100 veces mayor que el área del émbolo (A₁), la fuerza de salida (F₂) será 100 veces mayor que la fuerza de entrada (F₁).
Comprender las Compensaciones
Esta multiplicación de fuerza no viola las leyes de la física y no es una fuente de energía gratuita. Existe una compensación fundamental dictada por la conservación de la energía.
El Principio de Trabajo-Energía
En un sistema ideal, el trabajo realizado sobre el pistón de entrada debe ser igual al trabajo realizado por el pistón de salida. El trabajo se calcula como Trabajo = Fuerza × Distancia.
La Compensación de la Distancia
Debido a que la fuerza de salida (F₂) es mucho mayor que la fuerza de entrada (F₁), la distancia que se mueve el cilindro de empuje de salida (D₂) debe ser proporcionalmente menor que la distancia que recorre el émbolo de entrada (D₁).
Para levantar el enorme cilindro de empuje solo una pulgada, es posible que deba empujar el émbolo pequeño hacia abajo 100 pulgadas. Está cambiando un movimiento largo con baja fuerza por un movimiento corto con alta fuerza.
Tomar la Decisión Correcta para su Objetivo
Comprender este principio le permite aplicarlo a diferentes objetivos, ya sea en diseño, operación o simple comprensión.
- Si su enfoque principal es el diseño: Concéntrese en la relación de las áreas de los pistones (A₂/A₁), ya que esta relación determina directamente el factor de multiplicación de fuerza de su sistema.
- Si su enfoque principal es la operación: Reconozca que, si bien la fuerza generada es inmensa, el movimiento del cilindro de empuje será lento y deliberado. Esta compensación de fuerza por distancia es una característica operativa y de seguridad fundamental.
- Si su enfoque principal es la comprensión: La conclusión clave es que la presión permanece constante en un fluido cerrado, lo que permite que una fuerza pequeña sobre un área pequeña se convierta en una fuerza grande sobre un área grande.
Al dominar este principio, puede ver cómo la mecánica de fluidos simple permite algunas de las maquinarias más potentes del mundo moderno.
Tabla de Resumen:
| Componente | Función | Principio Clave |
|---|---|---|
| Émbolo (Pistón Pequeño) | Aplica la fuerza inicial (F₁) sobre un área pequeña (A₁) | Genera presión del sistema (P = F₁/A₁) |
| Cilindro de Empuje (Pistón Grande) | Ejerce la fuerza de salida multiplicada (F₂) sobre un área grande (A₂) | Convierte la presión en fuerza (F₂ = P × A₂) |
| Fluido Incompresible | Transmite la presión sin disminución a través del sistema | Núcleo de la Ley de Pascal |
| Multiplicación de Fuerza | La fuerza de salida es la fuerza de entrada multiplicada por la relación de áreas (F₂ = F₁ × (A₂/A₁)) | Se logra cambiando distancia por fuerza |
¿Necesita fuerza precisa y potente para sus aplicaciones de laboratorio? KINTEK se especializa en equipos de laboratorio de alta calidad, incluidas prensas hidráulicas diseñadas para brindar confiabilidad y rendimiento exigente. Ya sea que esté comprimiendo muestras, moldeando materiales o necesite una aplicación de fuerza personalizada, nuestra experiencia garantiza que obtendrá la herramienta adecuada para sus necesidades. ¡Contacte a nuestros expertos hoy mismo para encontrar la solución de prensa hidráulica perfecta para su laboratorio!
Guía Visual
Productos relacionados
- Horno de Prensado en Caliente por Inducción al Vacío 600T para Tratamiento Térmico y Sinterización
- Horno de Prensado en Caliente al Vacío Máquina de Prensado al Vacío Horno Tubular
- Horno Tubular de Cuarzo para Laboratorio de Alta Presión
- Horno de Sinterización y Tratamiento Térmico al Vacío con Presión de Aire de 9MPa
- Horno de tubo de cuarzo de laboratorio de 1400 ℃ con horno tubular de tubo de alúmina
La gente también pregunta
- ¿Es más barata la soldadura fuerte o la soldadura por fusión? Un análisis detallado de costos para su proyecto
- ¿Por qué las uniones soldadas están sujetas a fallas por fatiga? Comprender los factores críticos para uniones duraderas
- ¿Se puede producir un arco eléctrico en el vacío? Cómo el alto voltaje crea plasma en el vacío
- ¿Cuál es la ventaja de usar el conformado por prensado en caliente? Lograr piezas más resistentes y complejas
- ¿Qué productos se fabrican mediante prensado en caliente? Logre la máxima densidad y rendimiento para sus componentes
